|
Welcome back to Flipping the Focus.
Introduction In the last post (here), you read an interview, conducted by Flipping the Focus, with Ottawa Educator, Jaime DePippo (@MrsDePippo). The interview was Part 2 of a series that delved into the mindset and actions of an educator who is actively exploring the impact of the Thinking Classroom Framework (see Liljedahl, 2017) on student learning and teaching--in both Mathematics and English (Grades 9 and 10, Applied courses). |
"Students are capable, critical thinkers and problems solvers. If we deprive our students of these opportunities, they will not grow. Students need to be actively engaged in their learning."
This quote, in turn, lead us to the following wonderings:
1-What does this mean for educators' planning?
- Given that adolescents are more likely to respond faster emotionally than rationally, how can we better support their learning?
- How can we engage adolescents' understanding that it's difficult for them to 'override automatic responses' because their pre-frontal cortex is still maturing?
The remainder of this post focuses on these questions--that is, not in an effort to answer them: As pointed out by the last wondering, the goal is our own learning...through conversations about exploring where novelty 'fits' into our teaching practices.
As you continue with the information presented from both cognitive science and the Thinking Classroom, invite a colleague to read, reflect on practice, and discuss next steps with you.
|
"Cognitive Science...Meet the Thinking Classroom"
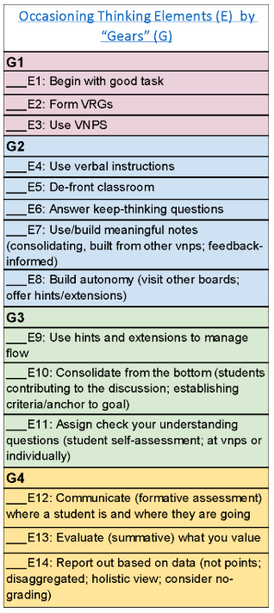
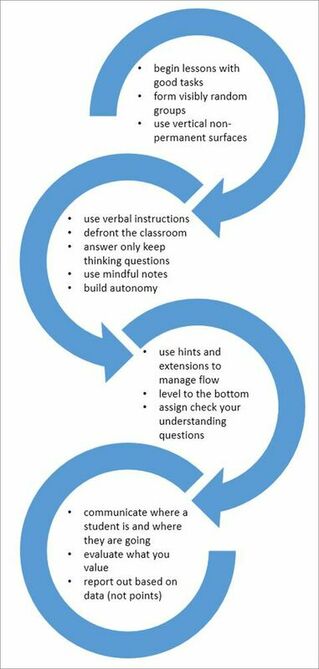
Thinking Classrooms In an earlier post, I listed and defined each of the elements (E) of the Thinking Classroom (here). These elements are clustered into, what Dr. Peter Liljedahl, refers to as gears. In the graphic (right), the 14 elements are colour-coded into their respective gear. Generally, as we evolve our pedagogical practice through the elements, we tend to begin with Gear 1 (G1) and progress by adding subsequent gears over time (G2 to G4). Cognitive Science Currently, I am helping support networked/regional professional learning around improving student outcomes in Mathematics through inquiry. The inquiries are being implemented by nine, district school boards in Eastern Ontario. These districts, for many years now, have been contributing to both networked learning and educational research through the Eastern Ontario Staff Development Network (EOSDN). A complementary resource that educators are studying is David A. Sousa's How the Brain Learns Mathematics. |
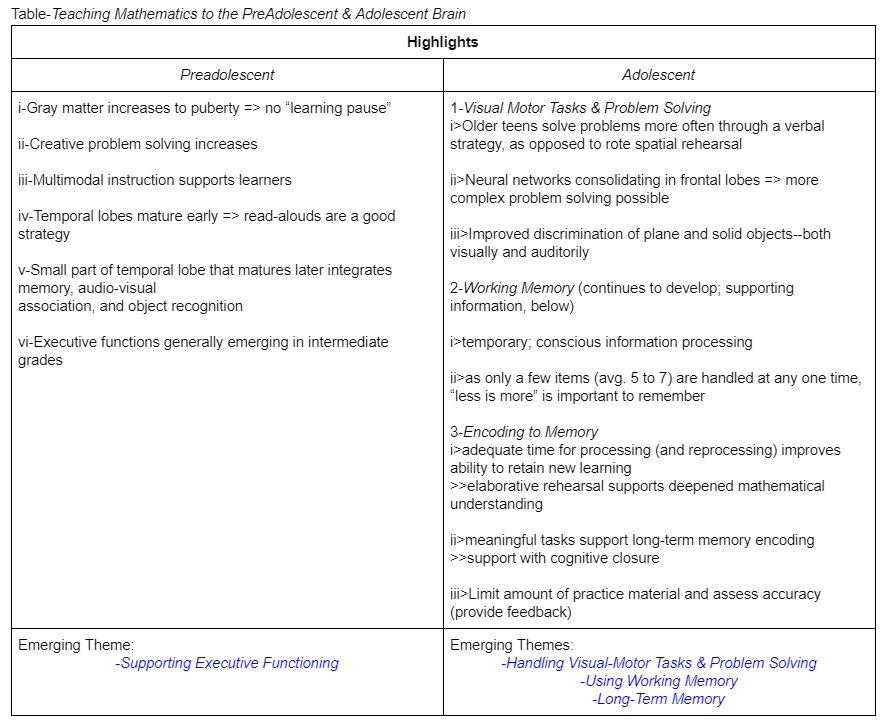
In the section that follows, I will present a draft of results of some coding that I completed between the framework and Chapters 5 & 6. In terms of my own interpretation, I am currently seeing that aspects of both cognitive science (CS) and Thinking Classrooms (TC) play a reciprocal role in student learning. That is to say, a TC pedagogy is more successfully enacted when we attend to preadolescent and adolescent brain development, while student cognition is supported by engaging students with the geared elements of the framework.
|
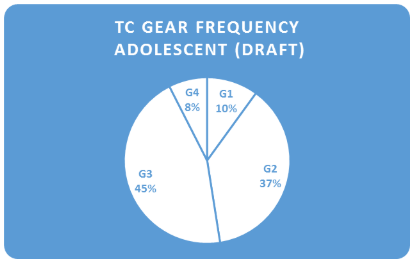
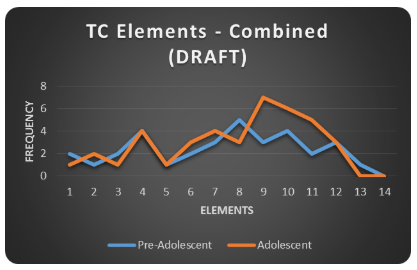
TC Elements-Adolescent
Figure 3 presents the frequencies for each of the 14 elements and for each stage in cognitive development--preadolescence and adolescence. The adolescent data portrays elements 9 through 11 as supporting adolescent cognition the most (i.e., "Gear 3")--specifically, managing hints and extensions; consolidating from the bottom; and student self-assessment. |
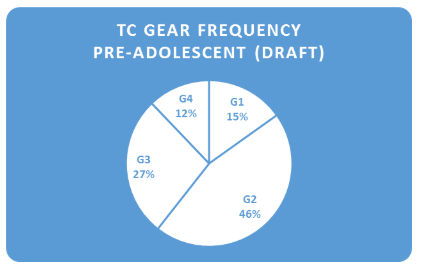
TC Elements-Preadolescent
Figure 3 also presents the frequencies for preadolescent learners. Notably, elements 4, 8 and 10 seem to be most influential in supporting preadolescent cognition (i.e., verbal instructions, building autonomy, and consolidating from the bottom, respectively), followed by elements 7, 9 and 12.
Before wading further into the complexity of these results, I would like to re-emphasize that these are drafted--i.e., they, on the basis of my interpretation, suggest how CS and TC are related. They also provide you with a glimpse into my own reflective practice: not only is this how I inquire, in part, into examining the value of pedagogical practice on student engagement and learning; it is also representative of the collaborative inquiries we can be doing alongside and in support of future-ready learners.
It's also important to consider those places where I have used the word, "most", in relation to support. For example, when thinking about the most frequently recorded skills for preadolescents, it's not that learners already 'arrive' with these abilities; rather, we use the elements to actively engage learners and support the development of their executive functioning. Similarly with adolescents, learners may not enter in to your class already expressing the skills encompassed by the emerging themes (table, above). What it does imply is that we can attend to planning and interacting with learners in ways that will bring about growth in these areas.
students of these opportunities, they will not grow. Students need to be
actively engaged in their learning."
With respect to planning instruction for all (Chapter 2; Learning for All, 2013), we might interpret Figure 1 as Gear 2 elements being more widely used to setting the foundation for more complex interactions between preadolescent learners with elements of the "Assessment Loop" (Causarano & Coulombe, 2018)--for example, establishing assessment capability for deepened learning through self-assessment, goal setting and monitoring towards attaining goals.
Moving towards adolescence, we might look upon the prevalence of Gear 3 elements as leveraging students' growing capacity to solving complex problems for deepening their conceptual understanding. We might also see how assigning fewer, meaningful "check your understanding" problems puts less strain on working memory, provides adequate time for elaborative rehearsal--lending itself also to developing procedural fluency.
Across all graphs (Figures 1 to 3), you'll note an under-representation of gear 1 and 4 elements. Gear 1 elements--good tasks, VNPSs and VRGs: these are the starting point for any educator's journey into enacting a TC pedagogy. Even for educators consistently practising Gear 4 elements, alongside their students, Gear 1 elements are a 'gateway' to engaging in deep, pedagogical practice. Notably, these elements can be implemented quickly and, perhaps, contribute indirectly--through classroom structures (physical space and groupings)--to student cognition. Gears 2 and 3 are comprised of a number of strategies that engage students to being active in their learning. Our engagement with these strategies means that we are consistently monitoring and communicating with learners over time. These actions, we might say, have direct impact on student learning and are more easily referenced against developmental markers from CS. Lastly, most of the Gear 4 elements relate to assessments of learning. These can be redressed by students and teachers in a formative manner but constitute a small amount of all assessments performed.
Beyond what has been presented in this post, there is so much that we can discuss and propose as inquiries that bridge the gap between the many opportunities we have to promote student learning and the actual learning that takes place for educators and their students.
In the opening, two wonderings were shared:
1-What does this mean for educators' planning?
- Given that adolescents are more likely to respond faster emotionally than rationally, how can we better support their learning?
- How can we engage adolescents' understanding that it's difficult for them to 'override automatic responses' because their pre-frontal cortex is still maturing?
As you move forward with your own journey into enacting a TC pedagogy, I believe the following might serve as good guiding statements:
- The Thinking Classroom can be enacted in such ways to support the development of student cognition.
- The Thinking Classroom supports what is currently known about cognitive science and brain maturation.
- When students understand how they learn and why a particular pedagogy is being used, they will be more likely to see themselves as confident and assessment-capable learners.
You can view the slide-deck below, as well as downloading your own copy that includes notes I've used in speaking about the material in this blog, as well as future, potential directions for collaborative and action-based research.
Prefer to listen to a presentation of the synthesis? View the slides in the form of video? See the button below to listen/view.
In closing, I can't help but to think of the conversations that can be inspired when we take collective action to improving student learning. As this blog is a means for readers to network and gradually change the context for how they teach and learn, we all benefit by drawing nearer to the perspectives shared here and shared beyond with our professional learning networks. Please feel free to share your comments and questions to this post using the "Leave a Reply" form provided, below.
I am more than happy to collaborate with you and make our learning visible, here, in this blog and across Flipping the Focus' social media platforms, as well as your own. If at any time, you have questions or comments, please feel free to reach out to me at Flipping the Focus.
Sincerely,
Chris Stewart, OCT
Education Leader at Flipping the Focus
Causarano, J., & Coulombe, H. (2018, September 14). The Assessment Loop: Merging Assessment and Instruction. Retrieved January 29, 2019, from https://harnessassessment.com/2018/09/04/the-assessment-loop-merging-assessment-and-instruction/
EduGAINS. (2013). Learning for All, A Guide to Effective Assessment and Instruction for All Students, Kindergarten to Grade 12. Retrieved from http://www.edugains.ca/newsite/Learning4All/whats_L4All.html
Liljedahl, P. (2017, October 17). Building a Thinking Classroom in Math. Retrieved from https://www.edutopia.org/article/building-thinking-classroom-math
Margaret Sinclair Memorial Award Lecture: Peter Liljedahl. (2019, February 14). Retrieved from http://www.fields.utoronto.ca/activities/18-19/Margaret-Sinclair-lecture
Sousa, D. A. (2008). How The Brain Learns Mathematics. Thousand Oaks, CA: Corwin.
Thinking Classrooms: An Interview with Jaime DePippo - Part 2 [Online Interview]. (2019, February 18).





 RSS Feed
RSS Feed


